Cartesian Genetic Programming (CGP)の概要とお試し実装
Cartesian Genetic Programming (CGP)の概要についてのまとめと、サンプル実装したソースコードの紹介です。Julian F. Millerの”Cartesian Genetic Programming”2章の内容をベースにまとめてあります(なお、本の1・2章がこのサイトで公開されています)。また、Githubで今回実装したソースコードを公開しています。
CGPは、ニューラルネットと同様与えられたデータセットを入力してその期待値(に近い値)を出力するような計算グラフを学習によって得る手法です。ニューラルネットでは最初にネットワーク構造を定義したうえでその係数を学習しますが、CGPの目的はネットワーク構造自体を求めるところにあります。また、ニューラルネットはバックプロパゲーションによる勾配降下を前提としているため、積和演算や微分可能なActivationなど決められた処理要素しか使えませんが、CGPは勾配を使わないので微分可否にこだわらず自由な処理要素を扱うことができます。
元々、遺伝的アルゴリズム(GA)というものがあり、それを用いた遺伝的プログラミング(GP)という手法がありました。GAは、人類や動植物が交配や突然変異を繰り返しながらよりよい遺伝子を後世に残すことで種を反映させてきた手法を、コンピュータ上のシミュレーションにより模倣することで最適化問題を解くという手法です。そして、GPはGAの手法を用いてツリー状の計算ネットワークを学習する方法です。GPではツリー状にしか計算ネットワークを組めないので、計算ノードの出力を複数のノードで利用することができない点が問題でした。CGPは、計算ネットワークを2次元のマトリックス状に組んで、その間を比較的自由な配線でつなぐことを可能にすることで、この問題点を解決したものです。2次元のマトリックス状というところがCartesian(デカルト座標)の名前の由来です。
CGPとは
CGPは、入力ノード、演算ノード、出力ノードの3種類のノードをグラフ状につないだ計算ネットワークです。例えば、以下に単純なネットワークの例を示します。この場合、入力ノードと出力ノードが2個ずつ(2次元)あり、それ以外のノードは演算処理を行う演算ノードになります。
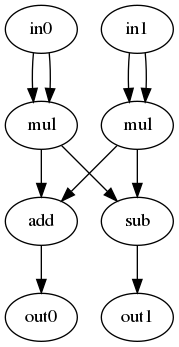
CGPを使うには、まず以下のものを定義する必要があります(この後、順番に説明していきます)。
- 演算ノードが行える演算の種類
- ネットワークのメタ構造
- 学習データと適応度関数
演算ノードが行える演算の種類
演算ノードとして用いる演算要素を決めます。これは例えば四則演算や、ロジック演算、またより高次の関数やテーブルなど、関数として表現できるものならなんでもよいです。画像処理なら様々なフィルタなどでもよいでしょう。使うつもりの演算(関数)のリストを用意します。それぞれの演算は複数の入力を持ってもよいですが、出力は1つのみである必要があります。入力引数の数をArityと呼び、Arityのリストも合わせて用意します。例えば以下のようなリストになります。
| 演算 | Arity |
|---|---|
| Add | 2 |
| Sub | 2 |
| Mul | 2 |
| Abs | 1 |
実装では、演算のリスト(ops)と引数の数のリスト(arities)を保持するClassを定義していて、例えば上記の演算リストであれば、以下のように登録します。
import operator
ops = cgp.operators([operator.add, operator.sub, operator.mul, operator.abs],
[2, 2, 2, 1])
ネットワークのメタ構造
CGPの目的は、最適なネットワーク構造(ノードの接続関係)を得ることでした。そのために、あらかじめマトリックス状に並んだ処理ノードを用意しておきノード間の配線を切り替えながら最適なネットワーク構造に近づけていきます。処理ノードの数は固定ですが、最終的に全ての処理ノードが使われるわけではなく、探索の途中で最大限使える処理ノードをマトリックス状に用意しておくという考え方です。
計算ネットワークは、入力ノード・処理ノード・出力ノードの3種類のノードと、それらを接続する辺からなります。入力ノード数は\(n_i\)個、出力ノード数は\(n_o\)個、そして処理ノードはそれらに挟まれて縦\(n_r\)個×横\(n_c\)個の2次元マトリックス状にならんでおり、それぞれ1~A本の入力と1本の出力を持ちます。Aは使われる全ての演算要素のArityの中の最大値です(実際には関数ごとにArityが違いますが、実装の都合上各ノードは最大Arity分の入力を持つことにします)。これらのノードをつないでいくことで、計算ネットワークを構成します。
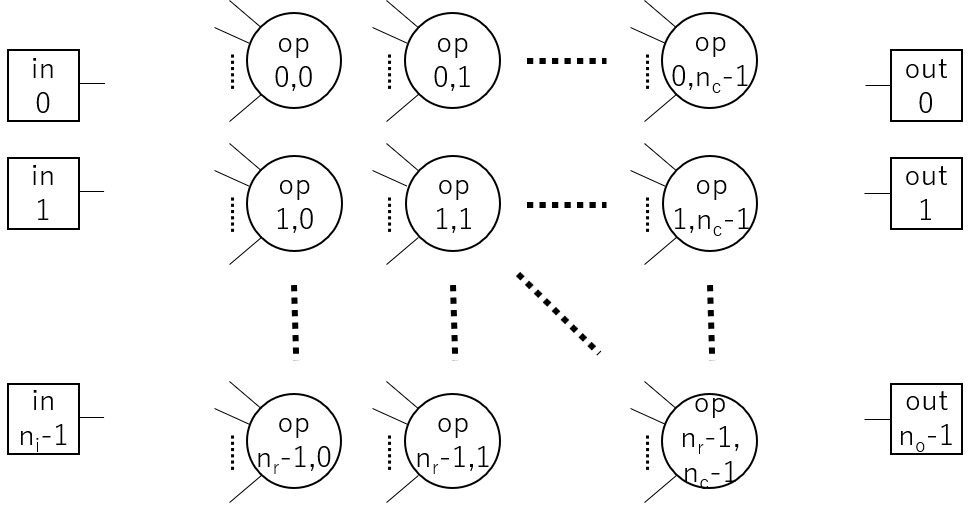
設定するパラメータは、入力ノード数(num_input)、出力ノード数(num_output)、演算ノード行数(rows)、演算ノード列数(cols)、Levels backというパラメータ(後述)、先ほど用意した演算ノードのリスト(ops)で、ソースコードでは以下のように設定しています。
my_genotype = cgp.genotype(num_input, num_output, rows, cols, levels_back, ops)
Levels backというのはある演算ノードがそのノードがいる列より何列前までのノードと接続可能かを示すものです。1なら直前の列からしか接続できないので、列毎に処理をして次の列に渡すというような(多くのニューラルネットのような)整然としたネットワークになります。一方でこれが大きいとどこからでも接続可能なので、雑然としたネットワークになりますが自由度が高い分表現できるネットワークの幅は広がります。
学習データと適応度関数
ニューラルネット同様、あらかじめ学習するための入力データと期待値データを用意しておきます。また、合わせて適応度関数を用意します。これはニューラルネットのLoss関数の逆でより大きくなるほうがよい関数になります。例えば以下のようなものです(期待値データ(exp)と出力データ(odata)の2乗和の符号反転したもの。この場合Lossのほうが自然な気はしますが・・・)
def func_fitness(exp, odata):
sum = 0.0
for e, o in zip(exp, odata):
sum += (e - o)**2
return -sum
CGPの学習
CGPの学習では、グラフ内のノード間の接続や演算ノードの種類をランダムに変えながらよりよいネットワーク構成を探索します。ノード間の接続関係は以下のような遺伝子型(Genotype)によって規定されます。演算ノード毎に、各引数が接続されるノードのアドレスのリストと演算の種類を表すインデックスを持ちます。また出力ノード毎に、そのノードが接続されるノードのアドレスを持ちます。
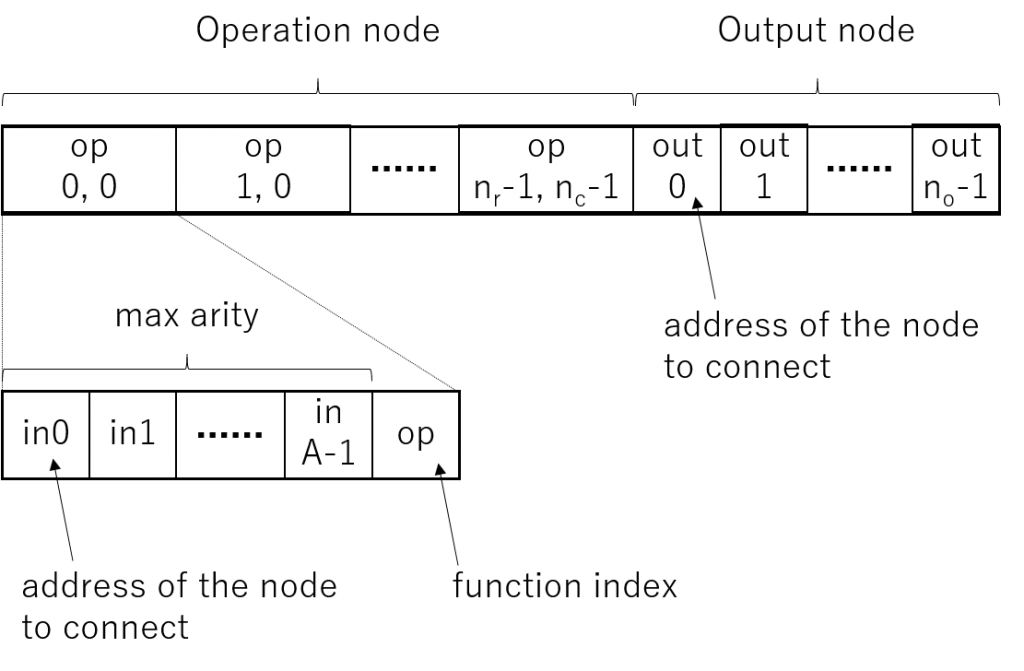
Miller本によると、CGPでは1+λアルゴリズムによる学習が一般的だそうです。これは1+λ個の個体(遺伝子型を持つグラフ)を用意し、それらのうちで最も適応度が高い個体(親)を選択します。そして、その個体の遺伝子型を突然変異させることで新たにλ個の個体を用意します。そして、親とλ個の子の中から新たに最も適応度が高い個体を選択するということを繰り返すことでより適応度の高い遺伝子型を探索するのです。ここで、突然変異とは、遺伝子型の中のいくつかの遺伝子(個々のアドレスや演算型を表す整数)をランダムに変えることを言います。一般的に、遺伝的アルゴリズムや遺伝的プログラミングでは、突然変異に加えて、交叉といって別の個体同士で遺伝子の一部を交換する操作を行うのですが、CGPではあまりいい結果が得られないそうで、突然変異のみの1+λアルゴリズムを薦めています。
実装では、以下のようにLoopを回して適応度の最大値を探索します。
max_fitness = -1.0e10
for i in range(num_generations):
fitness, parent_idx = cgp.find_best_genotype(genotypes, idata_list,
expdata_list, ops, func_fitness) # 適応度の高い個体を選択
if fitness >= max_fitness:
max_fitness = fitness
best_genotype = genotypes[parent_idx].copy()
genotypes[0] = genotypes[parent_idx].copy()
for j in range(1, num_genotype):
genotypes[j] = genotypes[parent_idx].copy()
genotypes[j].mutate(num_mutate, ops) # 突然変異
パラメータ設定
Millerによれば一度に突然変異させる遺伝子の個数は、全遺伝子数の1%程度がよいそうです。全遺伝子数とは演算ノードにおける演算の種別と接続先、それから出力ノードにおける接続先の数の合計です。例えば、2項演算のみを想定すると、演算ノードが100個あり出力ノードが10個あるとすれば、100 * (2 + 1) + 10 = 35個の遺伝子があるので、1%は3.1なので、3~4個ずつ突然変異させるのがよいことになります。ただし、小さいネットワークの場合は1%より多めのほうがよいようです(実際、1%が1以下になっていくというのもありますが、そのほうが収束性などもよいとのこと)。
ネットワークの行数・列数については、可能ならば1行にしてしまうのがよいそうです。1行にするのが最も接続の自由度が高くなります。もちろんこれはLevels backの設定の仕方にもよりますが、1行の時はそれなりに大きめの値にしておく必要があります。ただ、ハードウェアで回路を構成するなど、実際の結線に制約がある場合などは、行数を増やしてLevels backを小さめにとるのがよいでしょう。
実験
簡単な実験
まず、動作確認のために簡単な実験をしてみました。入力データと出力データはともに2次元で、以下の式を用いて学習データを作成しました。つまり以下の式が最終的な演算ネットワークとして構成されれば成功です。
$$f_{0}(x_{0},x_{1})=x_{0}^2+x_{1}^2$$ $$f_{1}(x_{0},x_{1})=x_{0}^2-x_{1}^2$$用いた演算ノードリストは、演算ノードリストの項で説明した、Add・Sub・Mul・Absです。適応度関数も、適応度の項で説明した差分の2乗和を用います。
以下の設定で学習を実施します。
- 演算ノード行数:2
- 演算ノード列数:2
- Levels back:2
- 個体数(1+λ):5
- 世代数:1000
- 突然変異数:2
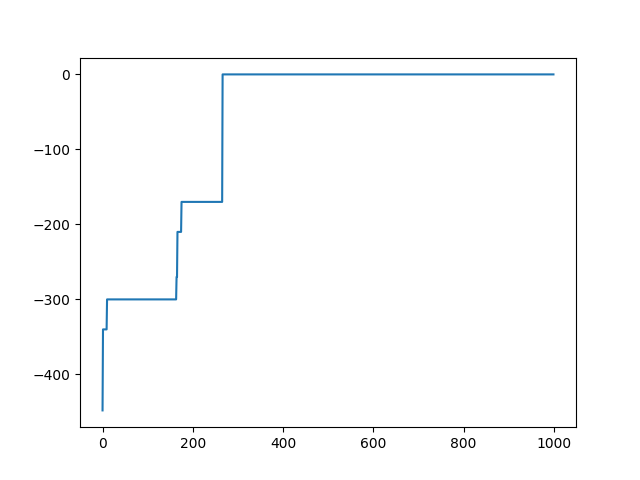
1000世代イタレーションを回したところ、適応度がゼロ(つまりエラーがゼロ)になりました。以下、1000世代分の適応度の変化を示します。ところどころで適応度がジャンプしているのが分かります。
結果として以下の回路が得られました。これはあらかじめ定義した正解関数と同じであることが分かります。
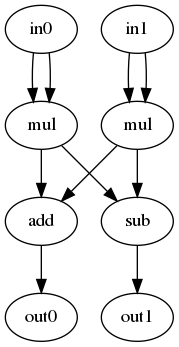
画像処理回路の生成
次にノイズ除去回路を生成してみます。学習用の画像としてMNISTの最初の30枚の画像を使います。MNIST画像を0~1に正規化したうえで、標準偏差0.1の正規ノイズをふかしたものを入力データに、元の画像を正解データに使います。適応度関数は、先ほどと同じ差分の二乗和です。
今回の実験では、入力ノード数及び出力ノード数は1です。1ノードがスカラー値ではなく画像を表すという設定です。演算ノードや適応関数が画像を引数にとるようにしておけば、このような使い方も可能です。演算ノードは、以下のものを用います。前半の単純な演算はnumpyの関数を用い、後半(Blurから先)はOpenCVの関数です(詳細はOpenCVドキュメントをご覧ください)。
| 演算 | Arity |
|---|---|
| Add | 2 |
| Sub | 2 |
| Mul | 2 |
| Abs | 1 |
| Blur | 1 |
| Dilate | 1 |
| Erode | 1 |
| Laplacian | 1 |
| Sobel(x) | 1 |
| Sobel(y) | 1 |
| Normalize | 1 |
まず、以下のパラメータで学習を行います。
- 演算ノード行数:2
- 演算ノード列数:2
- Levels back:2
- 個体数(1+λ):5
- 世代数:1000
- 突然変異数:2
1000世代回して、適応度が-39.78になりました。
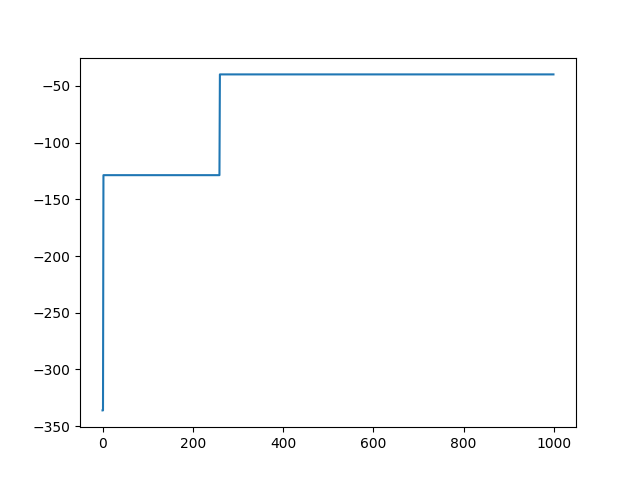
処理結果の画像が以下のようになります。



得られた回路が以下のようになります。
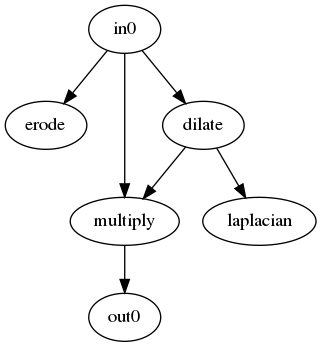
この結果は驚きです。普通ノイズ除去と言えば平滑化系の空間フィルタを使うものです。それにエッジ保存のためハイパスフィルタを組み合わせるような回路を予想していましたが、得られた回路はDilateと乗算という非常にシンプルな組合せでした。理由を考えてみるとMNISTという2値に近い画像だからだと思います。Dilateは2値画像を少し膨らませるのによく使います。膨らませた後で元画像をかけることで、数字部分は保存される気がしますし、平坦部もノイズが多少抑制されそうな気がします。なお、試しに自然画像であるCifar10でもやってみましたが、全く違う結果でした。Cifar10では単純にBlurを1回だけかける回路が作られ、ノイズは抑えられていますがぼやけてしまっていました。自然画像向けならもう少し演算ノードの種類を考えたほうがよさそうです。
さて、次にMNISTでの性能を上げるべく、より大きな回路で試してみました。
- 演算ノード行数:8
- 演算ノード列数:8
- Levels back:2
- 個体数(1+λ):5
- 世代数:10000
- 突然変異数:2
結果の適応度は-36.49で、ほんの少しだけ先ほどの結果より改善が見られましたが、かけたコストほどは改善しませんでした。これぐらいが限界なのかもしれないです。
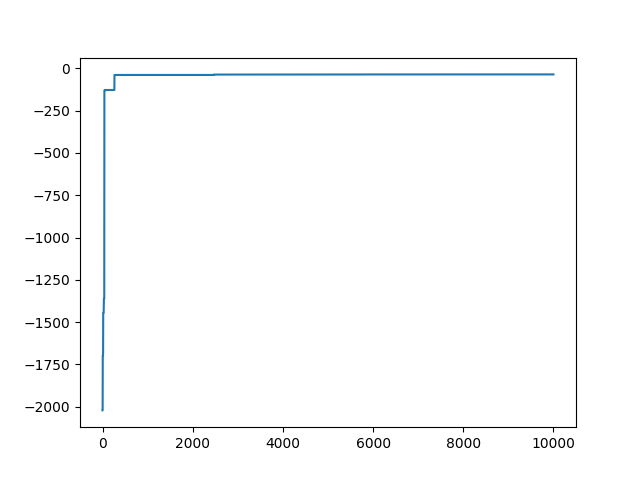
処理結果の画像は以下のとおりです。

得られた回路は以下のようになりました。
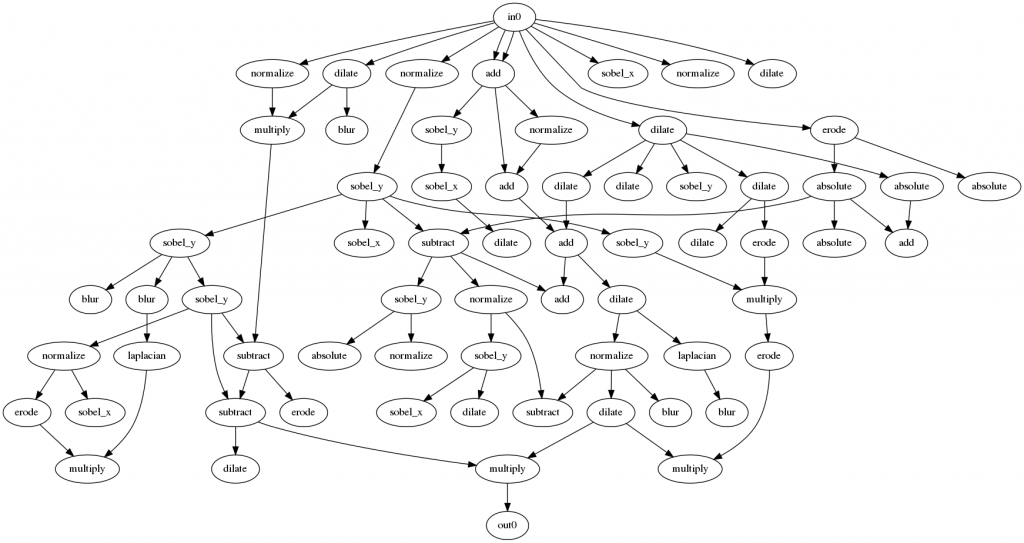
今回、大きな回路構成で行ったため、多くのノードが使われていないことが分かります。Millerによると、これらの使われないノードは意味があって、学習の途中に使われていないノードに切り替わることで、1つの遺伝子を変えただけでも大きな変更になり、世代の多様性を保っているそうです。
以上、CGPの概要とお試し実装でした。CGPはなかなか面白い技術ですが、いろいろ問題もありそうです。例えば、ニューラルネットと違い、勾配ベースではないので確かに最適な方向に向かっている感じがしません。収束も遅いです。また、今回の実装では定数を扱えません。GPで定数を扱うやり方はありますが、あまりスマートなやり方ではありません(dCGPというやり方は勾配ベースで定数を更新することができるので、期待できるかもしれませんが)。GPは、現在もいろいろな新しいやり方が生まれており、今後も改善の余地が多そうです。
参照
- CARTESIAN GENETIC PROGRAMMING(CGPの情報サイト、Miller本の1/2章公開)
- Julian F. Miller, “Cartesian Genetic Programming”(Miller本@Amazon)
- ソースコード(Github)
