強化学習の概要

強化学習とは最適な行動を学習するための手法

強化学習とは、ざっくり言えば「自動制御のための機械学習手法」です。自動制御というのは、自動車の自動操縦（自動運転）であったり、自律ロボットの移動であったり、またゲームをプレイするのも自動制御だと言えます。その際に、自動運転であればアクセル・ブレーキ・ステアリング操作が制御にあたりますし、ゲームであれば次の一手（もしくはコントローラの操作）が制御にあたります。では、自動制御をするにあたりどうなることが目的になるでしょうか。自動運転であればなるべく速く（場合によっては安く）目的地に到着することですし、ゲームであれば勝つことやよりスコアを高くすることが目的になります。さて、そのような制御をするにあたり、普通は何の手がかりもなしに制御をすることはしないと思います。運転であれば道路の状況や地図を確認しながら進む方向や速度を決めると思いますし、ゲームであれば現在の（将棋等の）盤面や（アプリ等の）画面を見ながら次の操作を考えると思います。このように、ある目的を達成するために、それぞれの状況（状態）においてどのような行動を選択することが最適なのかの指針（方策）を得る方法を強化学習と呼びます。

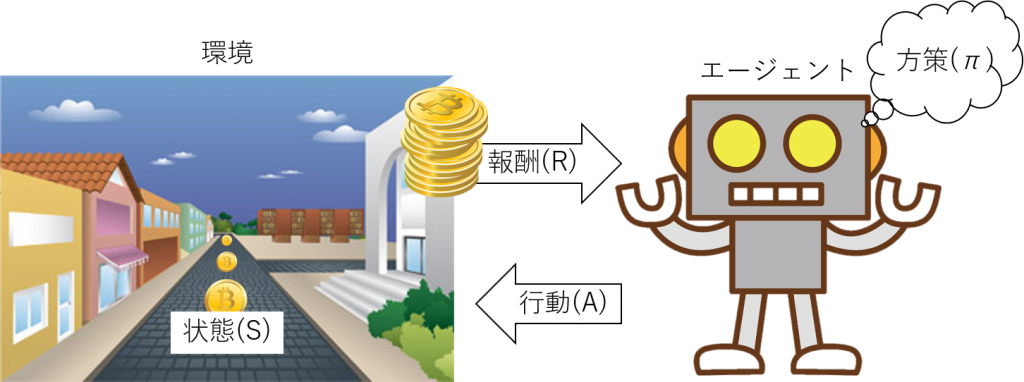
強化学習では、制御する側をエージェント、制御される側を環境と呼びます。例えば、仮想的な街の中をロボットが歩いてコインを集めるゲームを想像してください。この時、ロボットがエージェントで仮想的な街が環境にあたります。環境はその時その時によって状態を変えていきます。ゲームの例でいえば街の中のロボットやコインの位置が状態にあたるでしょう。そして、エージェントは環境の状態を読み取って、その状態に応じて行動（制御）を起こします（ある状態にある時にどのような行動を起こすかの指針を方策と呼びます）。そうすると、環境はエージェントに行動に応じた報酬を与えます。例えば、ロボットはコインの位置を読み取ってそっちの方向に動くという方策のもとに行動を行い、コインの場所にきたらコインという報酬を得るのです。環境の状態がエージェントの行動によってどのように変わるか、またどれぐらいの報酬をもらえるか、これらはあらかじめ決まっており、これを環境モデルと呼びます。もらえる報酬を最大化するような「方策」を見つけることが強化学習の目的です。

環境モデルとは「状態遷移」と「期待報酬」

まず環境モデルについて見ていきます。先ほどのロボットの例で考えると、ロボットがなんらかの行動を起こすたびに環境の状態が変わり、また報酬が得られます（コインを拾えない場合は報酬ゼロが得られると考えます）。ロボットがある時刻tにおいてある場所（ある状態）にいる時に、ある方向に動いた場合、次の時刻t+1においてロボットのいる場所は少し変わっているはずです。また、時刻t+1において何らかの報酬が得られているはずです。このように、行動の結果としてどのように状態が変化しどれぐらいの報酬が得られるかを規定する式を環境モデルと呼びます。

ここでは環境モデルを確率的なものと見立てて説明していきます。これは、実際の環境では何らかの外乱やノイズがあり、例えば前に進んだつもりでも少しよろけて斜め前に進んでしまうことも確率的にはなくはないだろう、という考えのもとで説明するということです。また、ここでは全ての変数は離散的なものとして考えます。例えば、ロボットの位置（状態）は自由な座標をとれるわけではなく、碁盤の目の交差位置のどれかにいるという前提を置いて考えます。連続な変数として考えることも可能ですが、ここでは簡単のため離散変数との前提で説明します。

環境モデルは、条件付き確率分布として以下のように書きます。

$$p(s’,r|s,a)$$

これは、例えばロボットがある場所sにいる時になんらかの行動aをとったら、次の時刻にロボットがどこにいて(s’)どれぐらいの報酬(r)がもらえそうなのかを表しています。確率分布なので、あくまでここにいてこれぐらいの報酬がもらえる確率がいくつ、という形で表現されます。目の前にコインがある状態で前に進めば、元々コインがあった場所に移動したうえでそのコインが報酬としてもらえる確率が高いということです。

また、この式だと状態と報酬がごっちゃになっていて使いづらいので、報酬の分を取り除いて純粋にどのように状態が遷移するかを表す状態遷移確率を以下のように計算しておきます。これは、環境モデルをrについて積算することで求められます（つまり、全ての報酬パターン（0コイン～M-1コイン）の確率を足してしまうということです）。

$$p(s’|s,a)=\sum_{r}p(s’,r|s,a)$$

逆に報酬だけを考えるために報酬の期待値を求めておきます。期待値とは簡単に言えば平均のことです。つまり、ある状態からある行動をとったら別の状態になったとして、そういった場合に平均的にもらえる報酬値のことで、環境モデルと状態遷移確率から以下のように求められます。

$$\begin{eqnarray} r(s,a,s’)&=&E[R_{t+1}|S_{t},A_{t},S_{t+1}] \\ &=&\sum_{r}r p(r|s,a,s’) \\ &=&\sum_{r}r\frac{p(s’,r|s,a)}{p(s’|s,a)} \end{eqnarray}$$

※本中の式ではΣが余計についています（そんな気がします・・）。

価値を推定して高めることが基本方針

さて、環境の中で価値を高めることが重要でした。ではどのように価値を表せばよいのでしょうか。基本的には得られる報酬を最大化したいということになりますが、報酬は持続的に何度も得られることになるので、目の前に見えているコインだけに着目していては近視眼的になり、大きな目標から外れてしまう可能性があります（例えば、進行方向にずっとコインが並んでいるように見えますがそれはそのうち途切れてしまい、むしろ逆方向に進むと見えない山の向こうに金塊が眠っているということもあるかもしれません）。そこで将来に渡ってもらえる報酬の和で考えるのがよさそうです。

ただ、問題にもよりますが何年もあとに得られる報酬と今現在得られる報酬を同列に考えるのはどうかと思います。そこで、将来もらえる報酬は現在もらえる報酬よりも割り引いて考えることにし、以下の式で価値を表すことにします（\(G_t\)が時刻tにおける価値、\(R_t\)が時刻tにおける報酬、\(\gamma\)は割引率で0以上で1より小さい数です）。

$$G_t=R_{t+1}+{\gamma}R_{t+2}+\gamma^{2}R_{t+3}+\cdots$$

状態価値関数

この割り引かれた報酬和を確率的な事象としてとらえて、ある状態における価値を条件付きの期待値として以下のように表します。これを状態価値関数と呼びます。

$$v_{\pi}(s)=E[G_{t}|S_{t}=s]=E[R_{t+1}|S_{t}]+\gamma E[G_{t+1}|S_{t}]$$

ここで、価値というのはある環境モデルの中である方策に則って行動した結果として得られるだろう報酬を合計したものなので、とった方策に依存しています。ここではとった方策を\(\pi\)で表しています。方策はある状態の時にどのような行動を選択するかということなので、状態の関数として表せますが、ここでは行動の選択についても確率的なものとして以下のように条件付き確率で表します（環境がノイズを含んでいる場合、エージェント側もある程度ランダム性を含んだ選択をするのがいいとも言えます）。

$$\pi(a|s)$$

状態価値関数は、状態遷移確率・報酬期待値・方策から以下のとおり計算できます（価値Gの定義から価値関数が再帰的に定義できることを使っています）。これを価値関数が従うベルマン方程式といいます。

$$\begin{eqnarray} v_{\pi}(s)&=&E[G_{t}|S_{t}=s] \\ &=&\sum_{a}\pi(a|s)\sum_{s’}p(s’|s,a)[r(s,a,s’)+\gamma v_{\pi}(s’)] \end{eqnarray}$$

ここで、本中の数式が一部理解できなかったので補足しておきます（細かい話なので次の行動価値関数の項まで飛ばし読みしてもだいじょうぶです）。状態価値関数は割引報酬和の期待値であり、割引報酬和は再帰的に書けるので状態関数は次の状態の状態関数を含む再帰的な式になりました。ただ、なぜ状態関数が単純に以下のようにならないかの説明が最初はよく理解できていませんでした。

$$v_{\pi}(s)=\sum_{a}\pi(a|s)\sum_{s’}p(s’|s,a)r(s,a,s’)+\gamma v_{\pi}(s’) ←これは間違い$$

なぜこうならないかというと、この第2項に必要とされているのは「t時点のs」に条件づけられた「t+1時点の割引報酬和」ですが、\(v_{\pi}(s’)\)というのは「t+1時点のs’」に条件づけられた「t+1時点の割引報酬和」だからです。そういう意味ではここを\(v_{\pi}(s)\)に変えても間違っており、\(v_{\pi}(s’)\)に遷移確率と方策をかけて周辺化するのが正しいやり方なのです。

行動価値関数

状態価値関数は、とった方策をもとに計算した価値なので、方策がうまくいったかどうかを表しているとも言えます。逆に、ある状態の時にある行動をおこなったらこれぐらいの価値がある、という関数があれば方策の選択に活かせる気がします。これを行動価値関数と呼び、状態価値関数と同様の以下のような式に従います。これを行動価値関数が従うベルマン方程式と呼びます。これは状態価値関数の計算の最後に方策の確率をかけて積算していた部分を除いたものだと分かります。

$$\begin{eqnarray} q_{\pi}(s,a)&=&E[G_{t}|S_{t}=s,A_{t}=a] \\ &=&\sum_{s’}p(s’|s,a)[r(s,a,s’)+\gamma v_{\pi}(s’)] \end{eqnarray}$$

さて、状態価値関数にしても行動価値関数にしても、ここまではそれらが従う方程式を定義しただけで、それらの実際の値が得られたわけではありません。価値関数の値を求めることは強化学習の直接の目的ではありませんが、目的のために必ず必要なことでもあります。そのため、様々なやり方でこれら価値関数の値を求めて（もしくはなんらかの関数で近似して）、強化学習の目的である価値の最大化につながる方策を得ようというのです。

強化学習手法の分類

強化学習の方法は、その問題設定や学習の手法によっていくつかの分類がされます（実際にはこれらの方法とDeep Learningを組み合わせるなど様々な手法が多数存在しますが、ここではこの本の2章に紹介されているものだけを列挙します）。

	価値ベース	方策ベース
モデルベース	価値反復法	方策反復法
モデルフリー	SARSA、Q学習など	方策勾配法、Actor-Critic法など

大きく分けると、環境モデルが既知（モデルベース）なのか、未知（モデルフリー）なのかによる分類です。既知（モデルベース）であれば、状態や行動の全てのパターンにわたって、直接的に価値関数の計算ができるので問題が比較的簡単になります。一方、未知（モデルフリー）の場合は、最初はある程度ランダムに行動を起こしてみて得られる報酬や状態遷移のサンプルをとり、それをもとに価値関数を推定する必要があるので一段階難しい問題になります。このような逐次的サンプリングによる価値関数推定の方法として、モンテカルロ法やTD学習などがあります。モデルフリー学習は、それらの手法をもとに最適な方策を求めるやり方です。

また別の分類軸として、「価値ベースの手法」か「方策ベースの手法」かというものがあります。その説明をする前に、もう一度強化学習の目的について考えてみます。強化学習の目的は、行動を繰り返すなかで得られる報酬の合計を最大化することです。そのためには、行動を行う時点でもらえる報酬だけでなく、将来にわたってどれぐらいの報酬が得られるかを考える必要があります。そういった将来に渡って得られる報酬の合計を「価値」と呼び、「価値」を最大化することを強化学習の目的にしています。つまり「価値」を高めるような「方策」をとれば目的が達成されるということになります。そのような「方策」を求めるにあたり、「価値」を求めたうえでその「価値」を高めるような「方策」を選択するやり方を「価値ベースの手法」と呼び、それに対してまず「方策」を決めてからその「方策」の「価値」を高めるように「方策」を改善していくやり方を「方策ベースの手法」と呼びます。

では、ここから強化学習の各手法を見ていきます。

モデルベース手法

まずは、より単純なモデルベース手法です。モデルが分かっているので、計算量やメモリ量さえ許せば比較的簡単な手順で問題を解くことができます。これらの手法の基本的な考え方として、状態価値関数は状態にのみ依存する関数なのでベルマン方程式の左辺と右辺に出てくる状態価値関数\(v_{\pi}(s)\)と(v_{\pi}(s’)\)は同じという事実を利用しています。これは、時刻tにおける期待価値と時刻t+1における期待価値が同じだと言っているように聞こえますが、実際には割引率の\(\gamma\)がかかっているため同じにはなっていません。ただ\(\gamma\)が1になると無限級数が収束しなくなるため、この議論が通じなくなるような気もします。

価値反復法

この方法では、行動価値関数が最大化される場合が最適（これを最適ベルマン方程式と呼ぶ）という考えのもと、状態価値から行動価値を求めそれを最大化することで状態価値を更新するというステップを繰り返しながら最適解に近づけます。価値反復法のアルゴリズムは以下のとおりです。

• 状態価値を適当な初期値に設定
• Loop:
  • モデルと状態価値から行動価値を求める
  • 状態毎に最大の価値を選択し状態価値とする
  • 収束したらLoopを抜ける
• 行動価値を最大化する方策を採用する

方策反復法

この方法では、状態ベルマン方程式の両辺に価値関数が現れることから、モデルや方策が分かっていれば価値関数について解析的に解くことができるという事実を利用しています。まず方策を適当に初期化しておいて、その方策をもとに価値関数を求めます。そしてその価値関数をもとに行動価値を計算し、行動価値を最大化するように方策を更新していきます。方策反復法のアルゴリズムは以下のとおりです。

• 方策を適当な初期値に設定
• Loop:
  • モデルと方策から、状態価値を解析的に求める
  • モデルと方策と状態価値から、行動価値を求める
  • 行動価値から、方策を更新する
  • 収束したらLoopを抜ける

モデルフリー手法

モデルフリーとは、状態遷移確率と期待報酬が分かっていない状態をいいます。つまり、ベルマン方程式にそって価値関数を計算することができません。そこで、実際に行動を起こしてみて得られる情報から価値関数を推定する手法がとられます。具体的には、1Step動くと状態が遷移するとともに報酬が得られますので、それらの情報をもとに価値関数を更新していけばよいのです。価値関数の定義は、今後得られる価値の割引報酬和の期待値でした。そう考えると、実際に行動してみた結果得られた報酬を各時点で積算し、それらの平均をとれば価値関数の推定値になりそうです。

価値関数の推定

さて、価値関数の推定のために実際に行動してみる必要があるということは、行動のための方策が必要になるということです。そして、価値関数は方策に依存するということを思い出してください。つまり、ここで推定する価値関数はとった行動の方策に応じた価値関数になるということです。ですから、適切な方策をとったうえで価値関数を推定することが大事になってきますが、それについては後程説明するとして、まずはある方策をとった場合の価値関数の推定を行います。

モンテカルロ法

モンテカルロ法では、価値関数の定義に忠実に割引報酬和を計算していき、全ての時刻における割引報酬和をその時点の状態毎に平均をとります。これは、問題がエピソードタスク（つまりゲームなどのように終わりがあるタスク）であると仮定すれば可能になります。エピソード長がT時間単位だと仮定すれば以下のような計算をすることになります。

$$V(s)=\frac{1}{N(s)}\sum^{T-1}_{t=0}G_{t}1(S_{t}=s)$$ $$N(s)=\sum^{T-1}_{t=0}1(S_{t}=s)$$

\(1(S_{t}=s)\)は、状態がsの時1でそれ以外の時0になる関数です。

ここで、分かりやすさのために一旦状態については忘れて割引報酬和の積算を書き下すと以下のようになります。

\(R_{1}\)	\(\gamma R_{2}\)	\(\gamma^2 R_{3}\)	\(\cdots\)	\(\gamma^{T-2} R_{T-1}\)	\(\gamma^{T-1} R_{T}\)
	\(R_{2}\)	\(\gamma R_{3}\)	\(\cdots\)	\(\gamma R_{T-3}\)	\(\gamma^{T-2} R_{T}\)
		\(R_{3}\)	\(\cdots\)	\(\gamma R_{T-4}\)	\(\gamma^{T-3} R_{T}\)
			\(\ddots\)	\(\vdots\)	\(\vdots\)
				\(R_{T-1}\)	\(\gamma R_{T}\)
					\(R_{T}\)

この表の各行のうち同じ状態のものの平均をとったものが価値関数の推定値になるということです。

さて、全ての報酬履歴から一気に平均値を求めてもよいのですが、次に説明するTD学習との整合性をとるために時刻0から逐次的に平均値を計算することを考えると、以下のような漸化式で計算していくことになります（この式で同じ結果が求められます）。

$$V_{t+1}(s)=V_{t}(s)+\frac{1}{N_{t+1}(s)}(G_{t}-V_{t}(s))1(S_{t}=s)$$ $$N_{t+1}(s)=N_{t}(s)+1(S_{t}=s)$$

\(\frac{1}{N_{t+1}(s)}\)は本来、時間が進むほど小さくなっていきます。それにより全ての要素に対して均等に平均をとることができるのですが、これを定数\(\alpha\)で置き換えればより最近の報酬和を重視した形の重み平均になります。例えば、エピソードの最初のほうと最後のほうで方策を徐々に変え、より後のほうの方策を重視したい場合などはこの方式のほうが都合がよくなります。

$$V_{t+1}(s)=V_{t}(s)+\alpha(G_{t}-V_{t}(s))1(S_{t}=s)$$

これは、\(G_{t}-V_{t}(s)\)を目標値\(G_{t}\)と現在値\(V_{t}\)の誤差と考え、 少しずつ現在値を目標値に近づけるような処理と考えられます。

TD法

モンテカルロ法では、累積報酬Gを目標値としてそれに近づけるように価値関数を更新しましたが、それには累積報酬を知っている必要がありそれはすなわち一度エピソードの最後まで行ってみないと更新ができないということになります。そこで、累積報酬和を現在得られている価値関数で代用するという方法をとればオンラインで逐次的に処理ができます。この方法をTD学習と呼びます。TD学習では目標値が\(G_{t}+\gamma V_{t}(s’)\)となり、誤差が\(G_{t}+\gamma V_{t}(s’)-V_{t}(s)\)となります。この誤差をTD誤差\(\delta\)と呼びます。

$$V_{t+1}(s)=V_{t}(s)+\alpha(G_{t}+\gamma V_{t}(s’)-V_{t}(s))1(S_{t}=s)$$

さて、この方法では最初のうちはごく少量のデータしか参照しないため、推定結果が偏る傾向が出やすいです。そこで何ステップか先までサンプリングした情報を利用することで偏りを軽減できます。これをn-ステップTD学習と呼びます。n-ステップ先までの収益\(G^{(n)}_{t}\)を以下のように定義します。

$$G^{(n)}_{t}=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots+\gamma^{n}V_{t}(S_{t+n})$$

n-ステップTD学習の更新式は以下のようになります。

$$V_{t+1}(s)=V_{t}(s)+\alpha(G^{(n)}_{t}-V_{t}(s))1(S_{t}=s)$$

この方法では、安定度が増した半面モンテカルロ法と同様にオンライン学習はできません。

TD(λ)法

TD(λ)法では新たなパラメータλを導入することで、n-ステップ学習のオンライン学習できないという欠点を改善しました。TD(λ)法では目標値をλ収益と呼び、以下のように定義します。

$$G^{\lambda}_{t}=(1-\lambda)\sum^{T-t}_{n=1}\lambda^{n-1}G^{(n)}_{t}+\lambda^{T-t}G_{t}$$

更新式は以下のとおりです。

$$V_{t+1}(s)=V_{t}(s)+\alpha(G^{\lambda}_{t}-V_{t}(s))1(S_{t}=s)$$

このTD(λ)法の目標値はなかなか意味が分かりにくいので、n=3の場合で考えてみます。その場合、TD(λ)法の目標値は以下のようになります。

$$(1-\lambda)G^{(1)}_{t}+(1-\lambda)\lambda G^{(2)}_{t}+(1-\lambda)\lambda^{2}G^{(3)}_{t}+\lambda^{3}G_{t}$$ $$=(1-\lambda)G^{(1)}_{t}+\lambda\left((1-\lambda)G^{(2)}_{t}+\lambda\left[(1-\lambda)G^{(3)}_{t}+\lambda G_{t}\right]\right)$$

つまり、まず全体を\((1-\lambda)\)と\((\lambda)\)に分けて、\((\lambda)\)側をまた\((1-\lambda)\)と\((\lambda)\)に分けてということをえんえんと続けるということです。これにより、\((\lambda)\)が0に近づくほど直近を重視し、1に近づくほど将来までを考慮することになります。 \((\lambda)\)が0の時TD学習に一致し、\((\lambda)\)が1の時モンテカルロ法と同様になるということです。

ではここで、TD(λ)誤差をTD誤差\(\delta\)で書き直してみます。まずその前にn-ステップTD誤差をTD誤差で分解してみます。分かりやすくn=2の場合を考えます。

$$\delta_{t+1}=R_{t+1}+\gamma V_{t}(S_{t+1})-V_{t}(S_{t})$$ $$\begin{eqnarray} G^{(2)}_{t}-V_{t}(S_{t})&=&R_{t+1}+\gamma R_{t+2}+\gamma^{2}V_{t}(S_{t+2})-V_{t}(S_{t}) \\ &=&\delta_{t+1}+\gamma\delta_{t+2}-\gamma\left[V_{t}(S_{t+1})-V_{t+1}(S_{t+1})\right]-\gamma^{2}\left[V_{t+1}(S_{t+2})-V_{t}(S_{t+2})\right] \\ &=&\delta_{t+1}+\gamma\delta_{t+2}+O(\alpha) \end{eqnarray}$$

\(O(\alpha)\)で近似した項は、別の時点の価値関数で同じ状態の価値を推定したものであり、\(\alpha\)が小さければ価値関数Vの変化も小さいとかんがえてもよいので\(O(\alpha)\)の誤差と考えてよいので、無視することができます。そして、同様にTD(λ)誤差についても以下のように書けることが分かります。

$$G^{\lambda}_{t}-V_{t}(S_{t})=\delta_{t+1}+(\lambda\gamma)\delta_{t+2}+\cdots+(\lambda\gamma)^{T-t-1}\delta_{T}+O(\alpha)$$

そして、TD(λ)誤差を時間t=0からt=T-1まで和をとると以下のようになります。

$$\sum^{T-1}_{t=0}\left(G^{\lambda}_{t}-V_{t}(S_{t})\right)1(S_{t}=s)=\sum^{T-1}_{k=0}\delta_{k+1}E_{k+1}(s)+O(\alpha)$$

\(E_{k+1}(s)\)は適格度トレースと呼ばれ以下で定義されます。

$$E_{k+1}(s)=1(S_{k}=s)+\lambda\gamma 1(S_{k-1}=s)+\cdots+(\lambda\gamma)^{k}1(S_{0}=s)$$

この和を計算するにあたり、見方を変えるとオンライン学習できることが分かるのですが、わかりやすくするためにモンテカルロの時と同様にこの和を書き下してみましょう。ここでも状態については気にせずに書いています。

\(\delta_{1}\)	\(\lambda\gamma\delta_{2}\)	\((\lambda\gamma)^{2}\delta_{3}\)	\(\cdots\)	\((\lambda\gamma)^{T-2}\delta_{T-1}\)	\((\lambda\gamma)^{T-1}\delta_{T}\)
	\(\delta_{2}\)	\(\lambda\gamma\delta_{3}\)	\(\cdots\)	\((\lambda\gamma)^{T-3}\delta_{T-1}\)	\((\lambda\gamma)^{T-2}\delta_{T}\)
		\(\delta_{3}\)	\(\cdots\)	\((\lambda\gamma)^{T-4}\delta_{T-1}\)	\((\lambda\gamma)^{T-3}\delta_{T}\)
			\(\ddots\)	\(\vdots\)	\(\vdots\)
				\(\delta_{T-1}\)	\(\lambda\gamma\delta_{T}\)
					\(\delta_{T}\)

さて、この表の縦方向が時間tを示し、各行が上からt=0からt=T-1に対応します。つまり時間毎の積算では未来の価値について積算を行うため、一旦終了までサンプルを終えないと積算が行えないことが分かります。これを前方観測的な見方と言います。しかし、やりたいことはこの表中の項目を全て積算したいということです。では、縦方向に足していってはどうでしょうか？ここでは横方向もある意味時間であるkを示し、各列が左からk=0からk=T-1に対応します。そこで時間ステップ毎に縦方向に積算していくことで、現時点でのTD誤差\(\delta\)のみを用いて積算していくことができるのです。これを後方観測的な見方と言います。これによりTD(λ)法ではオンライン学習が可能となるのです。

TD(λ)法の更新式は以下のようになります。

$$V_{t+1}(s)=V_{t}(s)+\alpha\delta_{t+1}E_{t+1}(s)$$ $$E_{t+1}(s)=\lambda\gamma E_{t}(s)+1(S_{t}=s)$$

---

価値ベースか方策ベースか

前にも述べましたが、方策を求めるためには2つのやり方があります。

• 行動価値関数Q(s,a)（Q関数と呼ぶ）を前項のどれかの方法で求め、その関数のもとで最適な行動を選ぶよう方策を改善
• 方策を直接的に推定して、状態価値関数Vによる評価により改善していく

なお、前項では状態価値関数Vを推定しましたが、同様のやり方で行動価値関数Qを推定することも可能です。

価値ベース手法

前項で説明した価値の推定は、実際に行動を起こしてみて報酬や状態遷移のサンプルを収集しながら行われました。ここでの行動は、なんらかの方策に則って行われるはずです。その時の方策はどのような方策にすればよいでしょうか？単純に求めたQ関数について最適な行動（greedyな方策という）をとったのでは、容易に局所解にはまってしまいます。そこで、たまにランダムな選択を織り交ぜることが有向だと知られています。ランダムな選択のことを「探索」、greedyな選択のことを「活用」と呼びます。εの確率でランダムに選択を行い、(1-ε)の確率でgreedyな選択を行う方針をε-greedy法と呼びます。

さて、方策が決まったとして、Q関数の推定にあたり方策の使いどころが2か所あります。1か所は、実際にとる行動を選択するために使う（挙動方策）というものですが、もう1か所はQ関数の更新計算を行うための状態や行動を選択するために使う（推定方策）というものです。必ずしもこれらに同じ方策を使う必要はありません。例えば、TD学習では価値関数の目標値を\(R_{t+1}+\gamma V_{t}(s_{t+1})\)として、そこに近づけるように価値関数を学習しましたが、ここで次の時刻の状態\(s_{t+1}\)は、現在の状態と同じとは限りません（一般的には違うものです）。そこで、考えを一歩進めて、実際に行動を起こした結果の\(s_{t+1}\)を使うのではなく、実際の行動と状態価値の更新を別物と考えたうえで、別の状態を使って価値関数を更新するということも考えられます。例えばランダムな探索を行いたい（挙動方策）のですが、それではなかなか価値関数が収束しないので、ランダムに探索をしつつも価値関数はgreedyな選択の結果で更新する（推定方策）というやり方などです。挙動方策と推定方策の両方に同じ方策を適用するやり方を方策オン型といい「SARSA」がそれにあたります。また別の方策を適用するやり方を方策オフ型といい「Q学習」がそれにあたります。

SARSA

TD学習法と同様のやり方でQ関数を更新ししたのち、ε-greedy法などにより方策改善を行っていきます。これらをQ関数及び方策が収束するまで行います。

Q学習

挙動方策のほうはSARSAと同様にε-greedy法などにより行いつつ、greedyな推定方策によりQ関数を更新するやり方です。

方策ベース手法

方策勾配法

方策をパラメタライズされた関数として表現し、価値のパラメータによる勾配を利用して、価値が高くなる方向に方策を改善していく方法です。

Actor-Critic法

方策だけでなく、価値関数もパラメータによりモデル化し（これをCriticと呼ぶ）、方策のモデル（これをActorと呼ぶ）とともに学習を行う方法です。